ACCORDION MUSIC: Advanced
(Continued from Intermediate Accordion Music)
13. From the Source to the Listener to Representation
Every area of interest has its own vocabulary, which people need to know in order to participate fully. Here are a few of the music terms you may find useful:
- Frequency measured in Hertz (Hz), duration of time measured in seconds (s), and intensity measured in watts per square meter, as used to describe a vibrating source and the tone(s) (sound wave(s)) it produces in the air.
- The corresponding terms pitch, duration of time indicated by the number or fraction of beat intervals, and loudness are used in describing music perception or interpretation by the brain, and the notes used to represent these on paper.
Frequency and Pitch: The relationship between a source's fundamental frequency and the brain's perception of pitch is not simple. Each accordion reed can vibrate in a complex manner, sometimes with higher harmonics or overtones, and can have a complicated attack and decay at the start and finish of a note. As well, each button push (or pull) simultaneously activates two (or more) reeds tuned slightly apart. All this contributes to the accordion's unique sound or "timbre". The brain's perception of pitch is influenced by all of this, and much more.
Tones and Notes: In addition to its association with sound waves and notes, the term tone has a second meaning in music, related to what we earlier called steps and baby-steps on a scale, where it can be used as an interval of pitch, such as that between the white keys C and D on a piano. Half that distance can then be called a semi-tone (the interval between the white key C and the black key C# immediately to its right). Which meaning is intended is usually clear from the context in which the term is used. The pitch and duration of a tone is shown on formal music sheets by the placement and shape of the note symbol that represents it, and this can be somewhat complicated; our accordion notation is much simpler.
Duration, Time and Beat-intervals: Sometimes it is useful to relate what we perceive as beat intervals to what we measure as a duration of the amount of time that a tone is held. This may be done using:
The two are related. For example, if the tempo is 60 bpm (60 beats in 60 seconds), then each beat represents a time interval of one second; however, if the tempo is 180 bpm (180 beats in 60 seconds), then each beat represents a time interval of one-third of a second.
One of the great things is that solo accordion players, just for the fun of it, are free to ignore tempo or pace recommendations, and play the tunes (and sing) as uniformly fast or as uniformly slow as they wish (or are able to).
- the measured tempo (or pace) which is the rate at which beats are counted, say, in beats per minute (abbreviated bpm).
- the length of a beat interval in seconds (abbreviated s), or fractions of a second.
The two are related. For example, if the tempo is 60 bpm (60 beats in 60 seconds), then each beat represents a time interval of one second; however, if the tempo is 180 bpm (180 beats in 60 seconds), then each beat represents a time interval of one-third of a second.
One of the great things is that solo accordion players, just for the fun of it, are free to ignore tempo or pace recommendations, and play the tunes (and sing) as uniformly fast or as uniformly slow as they wish (or are able to).
Intensity and Loudness: This, along with tempo (how fast or how slow), is an important part of the dynamics of a tune. The measurement of intensity, (say) in watts per square meter, of the musical sound wave as it reaches the listener depends on many factors, including the power delivered to the reeds by the player, and the distance of the listener from the source. Within the brain this is interpreted in terms of loudness, though in a non-linear way. Humans are more sensitive to mid-range sound frequencies than to low or high frequency sounds, and this also affects the perception of loudness. A measurement with a sound-meter using the (non-linear) decibel sound scale gives a result that is closer to the response and loudness perception of the ear and brain within particular ranges.
14. Standard Music Notation: Read and Ignore
Music experiences are primarily about playing tunes, singing songs, and listening to others playing and singing. For thousands of years, tunes and songs were passed on from one generation to the next, held in family or community memory, and this worked well for simple music on simple instruments. The past several centuries have seen the development of a wide range of more complex instruments, one of the most prominent of which is the piano, and more complex performances, such as those of symphony orchestras.
This occurred long before the advent of auditory recording and play-back devices (LP records, CDs, MP3, etc.), so they had to find a way of making a paper-based record of the music that was being composed and played. Hence the development of modern music notation with its staves and notes and a host of other symbols to represent musical keys, sounds and silences, relative pitches and their relative duration, rhythm, pace, and relative loudness, just to name a few.
Music experiences are primarily about playing tunes, singing songs, and listening to others playing and singing. For thousands of years, tunes and songs were passed on from one generation to the next, held in family or community memory, and this worked well for simple music on simple instruments. The past several centuries have seen the development of a wide range of more complex instruments, one of the most prominent of which is the piano, and more complex performances, such as those of symphony orchestras.
This occurred long before the advent of auditory recording and play-back devices (LP records, CDs, MP3, etc.), so they had to find a way of making a paper-based record of the music that was being composed and played. Hence the development of modern music notation with its staves and notes and a host of other symbols to represent musical keys, sounds and silences, relative pitches and their relative duration, rhythm, pace, and relative loudness, just to name a few.
|
The music notation at right is one of the simplest I could find; it is from one of Bethoven's symphonies. The three flats (b) indicate that it is in the key of Eb. The 2/4 time signature indicates that each beat is represented by a quarter (1/4) note, and there is the equivalent of two (2) beats in each bar. And so on .... and so on ....
Thousands of books, many with hundreds of pages, have been written on the topic of music and its standard notation. Whew! I get tired just thinking about it! |
15. Button-Accordion Notation: Read and Heed
The good news is that we can use my much simpler accordion notation, which includes the basic elements of each tune, while leaving much to the skill and imagination of the player. At the advanced level, the notation shows
- the pitch of notes to be played by their accordion button numbers.
- the relative duration of each note by simple punctuation marks before the button number.
- that some notes should be held longer than just indicated, by using a tilde ~ symbol.
- the bars (counting groups) of notes, using separated vertical bar lines.
- relative loudness, where necessary, by using larger bold fonts for louder and italics (without bolding) for quieter.
- notes that are to be played together smoothly (as a unit), by underlining.
- treble chords by placing the treble buttons to be pressed together inside square brackets.
- special attention or emphasis, where necessary, by placing the button number(s) inside (normal parentheses), prefixed by a subscript matched to a numbered explanation nearby.
- the time signature and tempo, normally indicated at the beginning of a tune.
16. Reheat of our Octave Alphabet Soup
The Pythagorean School of ancient Greece observed that there are some musical sounds that, though they differ in pitch, can seem remarkably similar to the human listener. They then proceeded to investigate the auditory space between these adjacent similar sounds, and observed that a lot of their Greek music was based on eight distinct sounds, the two end ones and six more that lay inside that space. Using the English alphabet, we might label the lower musical sound as "Note A" and the higher similar one as "Higher Note A". We could then write and count them, in increasing order, as follows:
A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 Higher A = 8
And the process could be repeated as we move on to even higher A's, counting to eight each time. Hence the use of the term "octave" meaning "eight". These represent the sounds of white keys on a piano.
Today, for historic reasons, we prefer to start with the sound that we label note "C", as follows
C = 1 D = 2 E = 3 F = 4 G = 5 A = 6 B = 7 Higher C = 8
We refer to this as the C collection of notes, and if played in the order given, starting and ending on C, we refer to it as the C-major scale.
If notes from this collection are played in order beginning and ending on A, we would refer to it as an A-minor scale.
When tunes are written using the C collection and with a focus on C as the "root" or "home" note, they tend to sound happy. When written using the C collection, but with a focus on A as the "root" or "home" note, they tend to sound sad or melancholic. Perhaps it's an over-simplification, but it does seem that major scales are mostly happy and up-beat, while minor scales are somewhat sad and melancholic.
The Greeks also observed that these sounds were NOT equally spaced in an relative auditory sense. Stepping from note to note on the C-major scale would be equivalent to the following:
C step-to D step-to E baby-step-to F step-to G step-to A step-to B baby-step-to higher-C
If we measured the frequencies of these tones, we would find that:
If you have a double-row accordion with a C row, that is what you are playing when you press the following buttons, pushing or pulling as indicated:
3 step-to 3* step-to 4 baby-step-to 4* step-to 5 step-to 5* step-to 6* baby-step-to 6
The Pythagorean School of ancient Greece observed that there are some musical sounds that, though they differ in pitch, can seem remarkably similar to the human listener. They then proceeded to investigate the auditory space between these adjacent similar sounds, and observed that a lot of their Greek music was based on eight distinct sounds, the two end ones and six more that lay inside that space. Using the English alphabet, we might label the lower musical sound as "Note A" and the higher similar one as "Higher Note A". We could then write and count them, in increasing order, as follows:
A = 1 B = 2 C = 3 D = 4 E = 5 F = 6 G = 7 Higher A = 8
And the process could be repeated as we move on to even higher A's, counting to eight each time. Hence the use of the term "octave" meaning "eight". These represent the sounds of white keys on a piano.
Today, for historic reasons, we prefer to start with the sound that we label note "C", as follows
C = 1 D = 2 E = 3 F = 4 G = 5 A = 6 B = 7 Higher C = 8
We refer to this as the C collection of notes, and if played in the order given, starting and ending on C, we refer to it as the C-major scale.
If notes from this collection are played in order beginning and ending on A, we would refer to it as an A-minor scale.
When tunes are written using the C collection and with a focus on C as the "root" or "home" note, they tend to sound happy. When written using the C collection, but with a focus on A as the "root" or "home" note, they tend to sound sad or melancholic. Perhaps it's an over-simplification, but it does seem that major scales are mostly happy and up-beat, while minor scales are somewhat sad and melancholic.
The Greeks also observed that these sounds were NOT equally spaced in an relative auditory sense. Stepping from note to note on the C-major scale would be equivalent to the following:
C step-to D step-to E baby-step-to F step-to G step-to A step-to B baby-step-to higher-C
If we measured the frequencies of these tones, we would find that:
- the frequency of note D is about 12% higher than that of note C; from C to D is one step.
- the frequency of note E is about 12% higher than that of note D; from D to E is one step.
- the frequency of note F is only 6% higher than that of note E; from E to F is thus a baby step.
If you have a double-row accordion with a C row, that is what you are playing when you press the following buttons, pushing or pulling as indicated:
3 step-to 3* step-to 4 baby-step-to 4* step-to 5 step-to 5* step-to 6* baby-step-to 6
|
Let's look at this another way. On a piano, this would be equivalent to starting from middle C (white key), and walking up the inside of the keyboard with your fingers, stepping over any black keys and touching only white keys, as follows. Observe that there is no black key between E and F, nor between B and C; hence the "baby-steps" when moving between these keys.
|
C black D black E baby step to F black G black A black B baby step to higher-C.
Remember the "Step Step Baby-step Step Step Step Baby-step" pattern; it defines what is called a diatonic major scale, and the notes form a diatonic collection. We will be applying this to other scales and collections shortly.
These auditory steps and baby-steps are not as visually obvious on an accordion, which is why I had to make use of a piano keyboard to develop the pattern. However, a finely tuned ear can distinguish between these auditory steps and baby-steps as the accordion is played.
Remember the "Step Step Baby-step Step Step Step Baby-step" pattern; it defines what is called a diatonic major scale, and the notes form a diatonic collection. We will be applying this to other scales and collections shortly.
These auditory steps and baby-steps are not as visually obvious on an accordion, which is why I had to make use of a piano keyboard to develop the pattern. However, a finely tuned ear can distinguish between these auditory steps and baby-steps as the accordion is played.
17. Adding Minor Spice to our Alphabet Soup
When your fingers walk up the inside of a piano keyboard, it takes only a "baby step" to move to the next key, but a full step to skip over a key. Starting from C and following this pattern you step only on white keys. A baby step is said to be equivalent to one-half a regular step.
When your fingers walk up the inside of a piano keyboard, it takes only a "baby step" to move to the next key, but a full step to skip over a key. Starting from C and following this pattern you step only on white keys. A baby step is said to be equivalent to one-half a regular step.
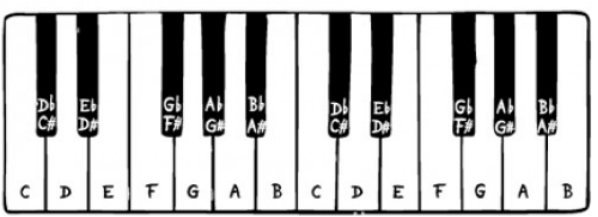
You may already know that white keys E (to F), and B (to C) are only a baby step apart. For the others, a baby step would take you to a black key.
The black key is higher pitched (sharper or spicier) than the white key immediately to its left. We use the # symbol to indicate sharper. For example C# and F# are the black keys immediately to the right of the C and F keys, as shown for piano keys at right.
Of course these black keys are also at a lower pitch (flatter) than the white key immediately to their right, for which the symbol b is used (such as Db, which is the same piano key (and sound) as C#, just written differently).
The black key is higher pitched (sharper or spicier) than the white key immediately to its left. We use the # symbol to indicate sharper. For example C# and F# are the black keys immediately to the right of the C and F keys, as shown for piano keys at right.
Of course these black keys are also at a lower pitch (flatter) than the white key immediately to their right, for which the symbol b is used (such as Db, which is the same piano key (and sound) as C#, just written differently).
Let us now walk up the inside of the keyboard starting from the white key D and following the "step, step, baby-step, step, step, step, baby-step" pattern:
D step-to E step-to F# baby-step-to G step-to A step-to B step-to C# baby-step-to higher-D
What we have here is the D collection of notes, and if written starting and ending on D, as above, it is known as the D-major scale. If you have an accordion with a D row, then you are playing the D-major scale when you play the following buttons:
3 step-to 3* step-to 4 baby-step-to 4* step-to 5 step-to 5* step-to 6* baby-step-to 6
You may note that this is identical to the buttons and steps in the previous section for the C-major scale. That is the great thing about true diatonic accordions: If you can play a tune on one row, you can play it on any other row, on any other true diatonic accordion. This easy transfer from one accordion key to another is called a transposition, and the accordion is known as a transposing instrument. Fantastic!
By the way, if we wrote the D collection of notes in succession starting and ending on B, it would sadly form a B-minor scale. To be more precise, it would form a B natural-minor scale; there are two other minor scales (melodic and harmonic).
In the music of western countries there are twelve (and twelve only) diatonic collections of notes. Master one, with its various scales or modes, and you have pretty well mastered them all.
D step-to E step-to F# baby-step-to G step-to A step-to B step-to C# baby-step-to higher-D
What we have here is the D collection of notes, and if written starting and ending on D, as above, it is known as the D-major scale. If you have an accordion with a D row, then you are playing the D-major scale when you play the following buttons:
3 step-to 3* step-to 4 baby-step-to 4* step-to 5 step-to 5* step-to 6* baby-step-to 6
You may note that this is identical to the buttons and steps in the previous section for the C-major scale. That is the great thing about true diatonic accordions: If you can play a tune on one row, you can play it on any other row, on any other true diatonic accordion. This easy transfer from one accordion key to another is called a transposition, and the accordion is known as a transposing instrument. Fantastic!
By the way, if we wrote the D collection of notes in succession starting and ending on B, it would sadly form a B-minor scale. To be more precise, it would form a B natural-minor scale; there are two other minor scales (melodic and harmonic).
In the music of western countries there are twelve (and twelve only) diatonic collections of notes. Master one, with its various scales or modes, and you have pretty well mastered them all.
18. Musical Keys
When we say that an outer row of a double-row G-C accordion is in the key of G, it means that buttons 2 to 11 yield sounds that correspond to the G collection of notes (G A B C D E F#). When we say that an inner row is in the key of C, it means that buttons 2 to 10 yield sounds matched to the C collection of notes (C D E F G A B).
You can, of course, play the C-row of your accordion in other keys (such as A-minor) and in other Greek modes that focus on home notes other than C and A. The major and minor keys correspond to two of the most common Greek modes. Perhaps not such a simple folk instrument after all?
When we say that an outer row of a double-row G-C accordion is in the key of G, it means that buttons 2 to 11 yield sounds that correspond to the G collection of notes (G A B C D E F#). When we say that an inner row is in the key of C, it means that buttons 2 to 10 yield sounds matched to the C collection of notes (C D E F G A B).
You can, of course, play the C-row of your accordion in other keys (such as A-minor) and in other Greek modes that focus on home notes other than C and A. The major and minor keys correspond to two of the most common Greek modes. Perhaps not such a simple folk instrument after all?
19. More Accidentals (on Purpose)
Consider a small ten-button single-row accordion in the musical key of G. All the notes from button 1 to button 10 may be in the G collection (G, A, B, C, D, E, F#), repeated to span nearly three octaves. I often find a tune that mainly uses the G collection, but contains a note or two, here or there, that isn't in this collection and thus isn't available on this small accordion. These notes, such as G#, A#, C#, D# and F, that are not part of the G collection, are called accidentals. This can present problems when playing certain tunes on a single-row G-accordion.
Similarly, all the notes on a single-row C accordion are from the C collection (C, D, E, F, G, A and B). The accidentals that might occassionally appear in tunes in this key are C#, D#, F#, G# and A#; these would be problematic for some tunes.
Today, I have a G-C dual-row accordion, with buttons 2 to 11 of the outside row in the musical key of G, and buttons 2 to 10 of the inside row in the key of C. However, button 1 on the outside row gives two mid-range notes (C# and D#), and button 1 on the inside row gives two mid-range notes (G# and A#), that are not in the C and G collections. These are included to help deal with the accidentals problem.
Since the F# is an accidental for the C-row, and the F is an accidental for the G-row, cross-playing between these rows can further reduce the accidentals problem.
Much of the time, all of this helps, but some tunes call for other notes that are not available on either row. When that happens you have to make a decision about skipping the accidental note, playing an alternate note (or notes), or just not playing the tune at all.
Consider a small ten-button single-row accordion in the musical key of G. All the notes from button 1 to button 10 may be in the G collection (G, A, B, C, D, E, F#), repeated to span nearly three octaves. I often find a tune that mainly uses the G collection, but contains a note or two, here or there, that isn't in this collection and thus isn't available on this small accordion. These notes, such as G#, A#, C#, D# and F, that are not part of the G collection, are called accidentals. This can present problems when playing certain tunes on a single-row G-accordion.
Similarly, all the notes on a single-row C accordion are from the C collection (C, D, E, F, G, A and B). The accidentals that might occassionally appear in tunes in this key are C#, D#, F#, G# and A#; these would be problematic for some tunes.
Today, I have a G-C dual-row accordion, with buttons 2 to 11 of the outside row in the musical key of G, and buttons 2 to 10 of the inside row in the key of C. However, button 1 on the outside row gives two mid-range notes (C# and D#), and button 1 on the inside row gives two mid-range notes (G# and A#), that are not in the C and G collections. These are included to help deal with the accidentals problem.
Since the F# is an accidental for the C-row, and the F is an accidental for the G-row, cross-playing between these rows can further reduce the accidentals problem.
Much of the time, all of this helps, but some tunes call for other notes that are not available on either row. When that happens you have to make a decision about skipping the accidental note, playing an alternate note (or notes), or just not playing the tune at all.
20. More Harmony: Accord and Chords
The Pythagorean School of ancient Greece observed that when certain notes were played together, they created a very pleasant sound, as though they were in harmony or accord with one another. You can test this on your accordion by pressing buttons 3, 4 and 5 simultaneously as you push the bellows together. If you are on the C row of a button-accordion, then you are simultaneously playing the three notes C, E, and G, which are the first, third and fifth notes of the C-major scale described earlier. Since these three notes are in accord with one another, we call them a chord. In fact, we name this after its major scale, and call this a C-major chord.
Interestingly you can get an inverted form of this C-major chord by pressing buttons 4, 5 and 6 on the push, and you are simultaneously playing the three notes E, G and higher C, which is still a C-major chord.
You can also obtain some chords on the pull of certain right-hand buttons; more about in later page(s).
If you play the first, third and fifth notes of any major scale, you will obtain a pleasant major-chord sound. That is how major chords are formed. For my diatonic button-accordions these notes are obtained from adjacent treble buttons (excluding button 1) on the push.
In addition, half of the buttons on the left side are single-button chords. For example, if you have a C-row on your accordion, you will find a C-major chord on the push of just one of the buttons on the left-hand side of the instrument; you will also find a G-major chord on the pull of that same button, and, sometimes, an F-major chord on a different button on the left-side. These three chords work well together, and are found in many tunes in the key of C.
Multi-row accordions usually have one or more minor chords on a single left-side button or buttons; again, more about this (briefly) on a later page.
All this gives a hint as to why "accordions" are called "accordions".
From the drop-down menu Advanced BUTTON LAYOUT, I'll show you how to find and identify all the chords on the left-hand side for the most common accordions.
Now it's time to move on for a brief look at the Button-ACCORDION LAYOUT itself.
The Pythagorean School of ancient Greece observed that when certain notes were played together, they created a very pleasant sound, as though they were in harmony or accord with one another. You can test this on your accordion by pressing buttons 3, 4 and 5 simultaneously as you push the bellows together. If you are on the C row of a button-accordion, then you are simultaneously playing the three notes C, E, and G, which are the first, third and fifth notes of the C-major scale described earlier. Since these three notes are in accord with one another, we call them a chord. In fact, we name this after its major scale, and call this a C-major chord.
Interestingly you can get an inverted form of this C-major chord by pressing buttons 4, 5 and 6 on the push, and you are simultaneously playing the three notes E, G and higher C, which is still a C-major chord.
You can also obtain some chords on the pull of certain right-hand buttons; more about in later page(s).
If you play the first, third and fifth notes of any major scale, you will obtain a pleasant major-chord sound. That is how major chords are formed. For my diatonic button-accordions these notes are obtained from adjacent treble buttons (excluding button 1) on the push.
In addition, half of the buttons on the left side are single-button chords. For example, if you have a C-row on your accordion, you will find a C-major chord on the push of just one of the buttons on the left-hand side of the instrument; you will also find a G-major chord on the pull of that same button, and, sometimes, an F-major chord on a different button on the left-side. These three chords work well together, and are found in many tunes in the key of C.
Multi-row accordions usually have one or more minor chords on a single left-side button or buttons; again, more about this (briefly) on a later page.
All this gives a hint as to why "accordions" are called "accordions".
From the drop-down menu Advanced BUTTON LAYOUT, I'll show you how to find and identify all the chords on the left-hand side for the most common accordions.
Now it's time to move on for a brief look at the Button-ACCORDION LAYOUT itself.

